Analytical approximations in probabilistic analysis of real-time systems

Abstract

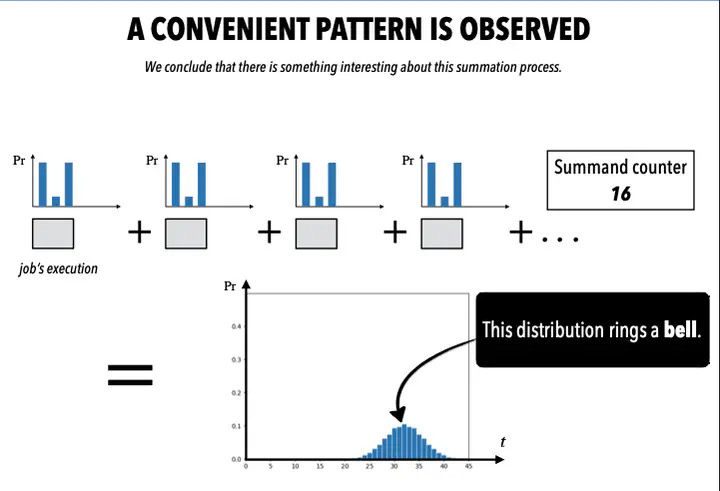
Probabilistic timing and schedulability analysis of real-time systems is constrained by the problem of often intractable exact computations. The intractability problem is present whenever there is a large number of entities to be analysed, e.g., jobs, tasks, etc. In the last few years, the analytical approximations for deadline-miss probability emerged as an important solution in the above problem domain. In this paper, we explore analytical solutions for two major problems that are present in the probabilistic analysis of real-time systems. First, for a safe approximation of the entire probability distributions (e.g., of the accumulated execution workloads) we show how the Berry-Esseen theorem can be used. Second, we propose an approximation built on the Berry-Esseen theorem for efficient computation of the quantile functions of probability execution distributions. We also show the asymptotic bounds on the execution distribution of the fixed-priority preemptive tasks. In the evaluation, we investigate the complexity and accuracy of the proposed methods as the number of analysed jobs and tasks increases. The methods are compared with the circular convolution approach. We also investigate the memory footprint comparison between the proposed Berry-Esseen-based solutions and the circular convolution. The contributions and results presented in this paper complement the state-of-the-art in accurate and efficient probabilistic analysis of real-time systems.

Filip Marković

Postdoc researcher in Computer Science

My research interests include real-time scheduling, probability theory and statistics, cyber-physical and embedded systems, and many more…